引言
由于控制理论与电力电子技术的飞速发展,使得
合愉电机多相电机的变频调速系统具有了比三相电机更多的突出优势:
(1)多相电机在缺相或故障情况下,由于具有比三相电机更多的控制自由度,可采用容错运行的方式,提高系统运行性能;
(2)减小系统转矩脉动幅值;
(3)采用低压,小容量器件实现大功率输出。
其突出的优点能很好的应用于轨道交通、电动汽车、航空航天等领域。双三相永磁同步电机由于具有以上的众多优势,近几年也被广泛的研究。
由于传统 PI 控制器无法做到无静差的跟踪交流量,文献[8]提出在 谐波子平面,通过同步旋转坐标变换,将 5、7 次谐波电流转换成直流量,再运用 PI 控制器对该直流量进行控制,虽然此方法能有效的抑制谐波电流,但需要进行多次的坐标变换,增加了算法的控制难度,系统过于复杂,且系统的鲁棒性受到影响。文献[9]采用在 子平面上运用两个准比例谐振控制器,对 5、7 次谐波电流进行抑制。但该方法只能对特定谐波进行抑制,且使系统运行性能降低。
为了解决上述问题,本文提出了一种改进的一阶线性自抗扰控制算法,通过六维空间矢量变换,将 子平面上的 5、7 次谐波电流经同步坐标变换转化为 子平面上的 6 次交流量,然后采用一阶 LADRC 设计电流环,并通过 BP 神经网络对自抗扰控制器的参数进行优化,以达到对谐波子平面上的全频域的谐波电流进行抑制。
1 双三相永磁同步电机数学模型
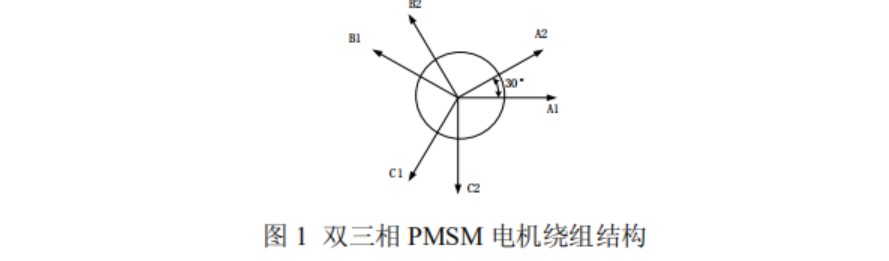
双三相永磁合愉同步电机的结构图如图 1 所示,该电机由 A1、B1、C1 和 A2、B2、C2 两套三相绕组构成,每套定子绕组互差 30°电角度且在空间上对称分布,单独一套绕组的各相在空间上互差 120°电角度且都成 Y 型连接,两套绕组的中性点相互隔离。双三相 PMSM 在静止坐标系下,其数学模型是一个多变量、非线性、强耦合系统且十分复杂。结合文献[10],经过上述静止坐标变换,双三相 PMSM 的 子平面对应式 1 中的前两行,该电机的基波和 v = 12k ± 1( k= 1,2,3…)次谐波都被映射到这个子平面上;v = 6k ± 1( k=1,3,5…)次谐波被映射 子平面,对应式 1 的中间两行,v = 3k ± 1( k= 1,2,3…)次谐波被映射 子平面,对应式 1 的最后两行。
2 谐波电流抑制策略
由于传统的 PI 控制器无法对交流量做到无静差跟踪,对谐波电流的抑制策略过于复杂,而准 PR 控制器又只能对特定次数的谐波进行抑制,对整体的谐波抑制效果不明显。因此,本文提出一种一阶 LADRC 控制器,来对谐波子平面上全频域的谐波电流进行抑制,其中最主要的是抑制 5 次和 7 次谐波电流。
3 仿真分析
为了验证一阶 LADRC 对谐波电流抑制能力,本文以一台额定功率 P=2KW 的双三相永磁同步电机为研究对象。在 Simulink 中参照双三相永磁同步电机的数学模型建立其仿真模型。电机定子电阻为 1.2Ω,极对数为 3,永磁体磁链为 0. 08Wb,漏感为 0.008m H,交、直轴电感为 0.01 m H。直流母线电压取 150V,系统给定转速为 130r/min,电机负载转矩为 15N•m。
4 结论
本文为了抑制双三相永磁
合愉同步电机谐波电流,改善电流波形,降低电机损耗,提出了线性 ADRC 控制方法,推出一种新的同步旋转坐标变换,在 子平面设计两个一阶线性自抗扰电流环。通过大量的仿真验证,将线性 ADRC 与传统的 PI 控制以及准比例谐振控制相比较。仿真结果表明,在 子平面采用线性 ADRC 控制可以大幅度的降低 5、7 谐波电流,降低电机损耗。